urlcolor = blue,
citecolor = blue,
breaklinks]hyperref
Обобщенные динамические уравнения плоского криволинейного движения материального тела по желобу с учетом сил трения (их численный анализ в некоторых частных случаях)
С. О. Гладков,
sglad@newmail.ru
С. Б. Богданова
sonjaf@list.ru.
Московский авиационный институт (национальный исследовательский университет) (МАИ)
Россия, 125993, Москва, Волоколамское шоссе, д. 4
В работе приведен вывод общих динамических уравнений плоского криволинейного движения с учетом сил как вязкого, так и сухого трения. Получена замкнутая система четырех нелинейных дифференциальных уравнений и проанализировано ее решение в некоторых частных случаях. Дана графическая иллюстрация различных траекторий для плоско--параллельного криволинейного движения.
05.45.-a. УДК: 531.332.1.
криволинейное движение, закон сохранения момента импульса, нелинейные динамические уравнения.
ВВЕДЕНИЕ
При внимательном знакомстве с теоретическими исследованиями, посвященными изучению свойств криволинейного движения [1,2,3,4,5,6,7], был обнаружен факт отсутствия общих динамических уравнений, описывающих плоское криволинейное движение при учете диссипативных свойств реальной физической среды. Надо сказать, что когда в классической механике принимаются во внимание силы трения, траектория движения становится, во--первых, финитной, а, во--вторых, качественно значительно более сложной, в чем можно убедиться, например, по работе [8], где аналитически и численно была решена задача о выяснении траектории движения для брахистохроны с трением. К слову сказать, именно эта задача и послужила толчком к обобщению полученных в ней результатов для вывода полной системы динамических уравнений материального тела массой $m$ с учетом сил трения и на случай двухмерного произвольного криволинейного движения.
ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ
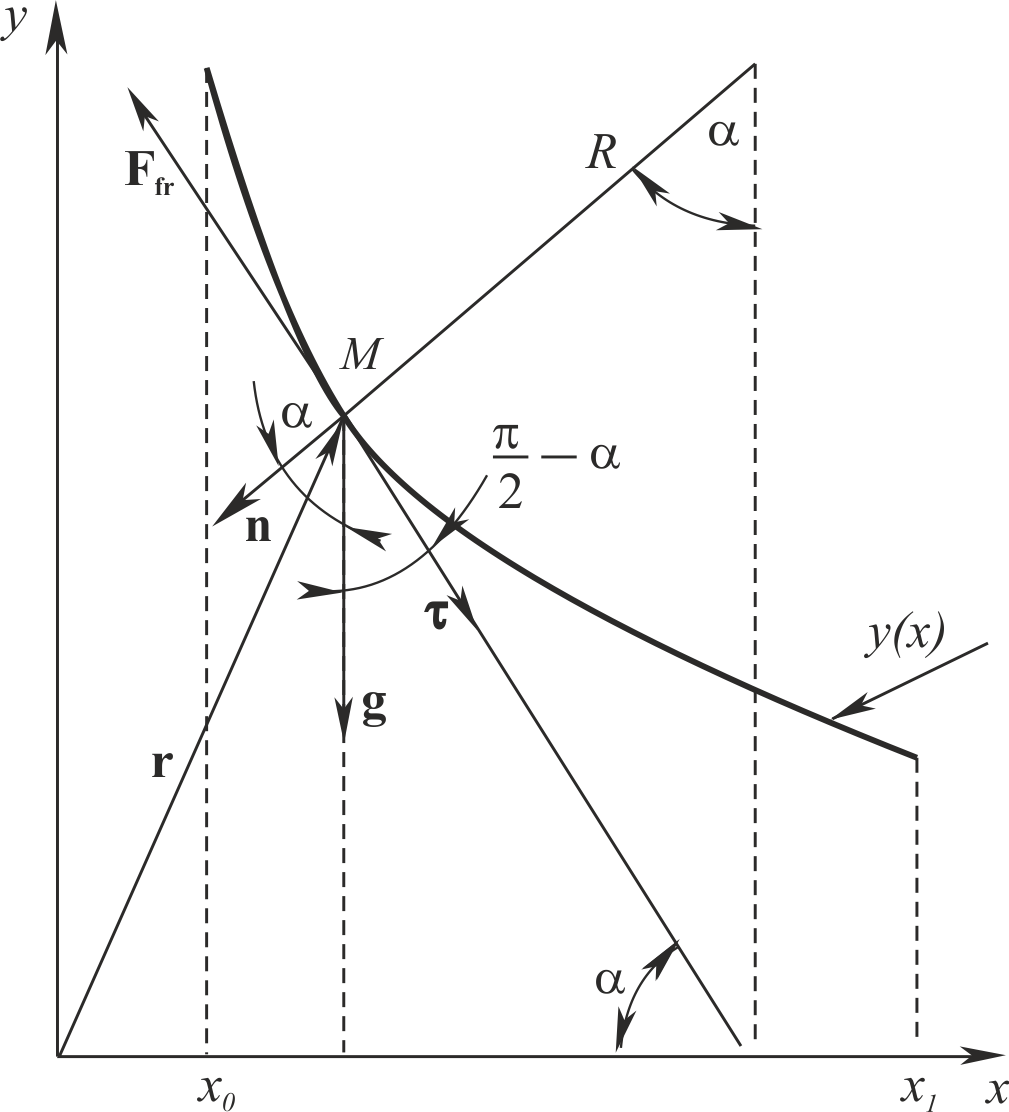
Рассмотрим произвольный кусок криволинейной траектории, показанный на рис. 1.
В подвижной системе координат, которую мы зададим двумя единичными векторами $\mathbf{n}$ и $\boldsymbol{\tau }$, где $\mathbf{n}$ --- единичный вектор нормали к траектории, а $\boldsymbol{\tau }$ --- единичный вектор касательной к ней по направлению движения, по аналогии с работой [8] можно записать следующую систему уравнений
$$ \label{GrindEQ__1_} \left\{\begin{array}{l} {\dot{v}=g\sin \alpha -\dfrac{F_{fr} }{m} ,} \\[4pt] {\dfrac{v^{2} }{R} -g\cos \alpha =\dfrac{N}{m} ,} \end{array}\right. $$
где сила сопротивления $F_{fr} =k_{1} N+F_{s} $, здесь $k_{1}$ --- коэффициент сухого трения, а $F_{s}$ --- сила вязкого сопротивления со стороны среды. Выберем ее в виде закона Стокса, то есть просто пропорциональной скорости движения, и положим, что $F_{s} =k_{2} v$, где по порядку величины коэффициент $k_{2} $ есть факторизованное выражение $\xi \eta L$, где $\xi$ --- числовой коэффициент, который для шара равен $3\pi $, $\eta$ --- динамическая вязкость среды, а $L$ --- линейный размер тела (для шара это просто $2R_{0} $, где $R_{0}$ --- радиус шара). $R$ --- радиус кривизны траектории в рассматриваемой точке, $N$ --- сила реакции желоба, по которому движется тело. Если желоб отсутствует, силу реакции следует положить равной нулю и учесть только сопротивление со стороны вязкой среды, т. е. только силу $F_{s} $.
В раскрытой форме систему уравнений fGrindEQ__1_ можно представить как
$$ \label{GrindEQ__2_} \left\{\begin{array}{l} {\dot{v}+\dfrac{k_{2} }{m} v-k_{1} \dfrac{v^{2} }{R} =g(\sin \alpha -k_{1} \cos \alpha ),} \\[5pt] {\dfrac{v^{2} }{R} -g\cos \alpha =\dfrac{N}{m} .} \end{array}\right. $$
В общем случае, когда исследуется динамика криволинейного движения по произвольной траектории, систему уравнений fGrindEQ__2_ следует дополнить еще одним уравнением. Речь идет об уравнении движения вектора момента импульса. Действительно, имеем для него
$$ \label{GrindEQ__3_}\dot{\mathbf{L}}=\mathbf{M}, $$
где момент импульса тела относительно центра неподвижной системы координат $(x,y)$ есть $\mathbf{L}=m\left[\mathbf{r}\times \mathbf{v}\right]$, а $\mathbf{M}=\sum _{i=1}^{n}\mathbf{M}_{i} $, где отдельный момент сил относительно центра координат $\mathbf{M}_{i} =\left[\mathbf{r}_{i} \times \mathbf{F}_{i} \right]$, $\mathbf{r}_{i}$ --- радиус--вектор $i$--ой силы $\mathbf{F}_{i} $. Для $z$--компоненты уравнения fGrindEQ__3_ имеем
$m\dfrac{d}{dt} \left[vr\sin \left(\alpha -\phi \right)\right]=mgr\cos \phi +$ $+Nr\cos \left(\alpha -\phi \right)-F_{fr} r\sin \left(\alpha -\phi \right)$.
Записывая левую часть этого уравнения, как
mdt =
=mr ( - )+mvdt
и учитывая верхнее уравнение в системе fGrindEQ__1_, после простых преобразований получим
$$ \label{GrindEQ__4_}-mgr\cos \alpha \cos \left(\alpha -\phi \right)+mv\frac{d}{dt} \left[r\sin \left(\alpha -\phi \right)\right]=\\ =Nr\cos \left(\alpha -\phi \right).
$$
Подставляя в fGrindEQ__4_ из нижнего уравнения системы fGrindEQ__2_ $N$, найдем в итоге следующую систему динамических уравнений
$$ \label{GrindEQ__5_} \left\{\begin{array}{l} {\dot{v}+\dfrac{k_{2} }{m} v+k_{1} \dfrac{v^{2} }{R} =g(\sin \alpha -k_{1} \cos \alpha ),} \\[5pt] {-gr\cos \alpha \cos \left(\alpha -\phi \right)+v\dfrac{d}{dt} \left[r\sin \left(\alpha -\phi \right)\right]=}\\ \hspace{35pt}{=\left(\dfrac{v^{2} }{R} -g\cos \alpha \right)r\cos \left(\alpha -\phi \right).} \end{array}\right. $$
После простого сокращения в левой и правой частях нижнего уравнения, а также после раскрытия производной по времени, получаем для него
$$ \label{GrindEQ__6_}v\dot{r}\sin \left(\alpha -\phi \right)+vr\left(\dot{\alpha }-\dot{\phi }\right)\cos \left(\alpha -\phi \right)= \\ =\frac{v^{2} }{R} r\cos \left(\alpha -\phi \right).
$$
Как было показано в [8], для элемента длины траектории имеет место равенство $dl=Rd\alpha $. Поэтому $v=R\dot{\alpha }$ или $\dot{\alpha }=\dfrac{v}{R} $. Подстановка этого соотношения в левую часть уравнения fGrindEQ__6_ приводит к еще одному сокращению, и в результате у нас получается совсем компактное уравнение $\dot{r}\sin \left(\alpha -\phi \right)=r\dot{\phi }\cos \left(\alpha -\phi \right)$. Таким образом, система уравнений fGrindEQ__5_ с учетом равенства $R=\dfrac{v}{\dot{\alpha }} $ может быть записана как
$$ \label{GrindEQ__7_} \left\{\begin{array}{l} {\dot{v}+\dfrac{k_{2} }{m} v+k_{1} v\dot{\alpha }=g(\sin \alpha -k_{1} \cos \alpha ),} \\[5pt] {\dot{r}=r\dot{\phi }\operatorname{ctg}\left(\alpha -\phi \right).} \end{array}\right.
$$
Далее, так как $v=R\dot{\alpha }=\frac{dl}{dt} =\sqrt{\dot{r}^{2} +r^{2} \dot{\phi }^{2} } $, т. е. $R^{2} \dot{\alpha }^{2} =\dot{r}^{2} +r^{2} \dot{\phi }^{2} $, а в полярной системе координат $r,\phi $ радиус кривизны может быть записан в виде
$$ \label{GrindEQ__8_}
R=\frac{\left(\dot{r}^{2} +r^{2} \dot{\phi }^{2} \right)^{\frac{3}{2} } }{2\dot{r}^{2} \dot{\phi }+r\dot{r}\ddot{\phi }-r\ddot{r}\dot{\phi }+r^{2} \dot{\phi }^{3} } ,
$$
после возведения формулы fGrindEQ__8_ в квадрат из уравнения $R^{2} \dot{\alpha }^{2} =\dot{r}^{2} +r^{2} \dot{\phi }^{2} $ немедленно находим
$$ \label{GrindEQ__9_}\left(\dot{r}^{2} +r^{2} \dot{\phi }^{2} \right)\dot{\alpha }=2\dot{r}^{2} \dot{\phi }+r\dot{r}\ddot{\phi }-r\ddot{r}\dot{\phi }+r^{2} \dot{\phi }^{3} .
$$
С помощью соотношения $v^{2} =\dot{r}^{2} +r^{2} \dot{\phi }^{2}$ и $r^{2} \dot{\phi }^{2} =v^{2} -\dot{r}^{2}$ имеем из fGrindEQ__9_
^2 =2^2 +r-r+(v^2 -^2 )
или
$$ \label{GrindEQ__10_}\dot{\alpha }-\dot{\phi }=\frac{\dot{r}^{2} \dot{\phi }+r\dot{r}\ddot{\phi }-r\ddot{r}\dot{\phi }}{v^{2} } .
$$
Чтобы преобразовать fGrindEQ__10_, воспользуемся нижним уравнением системы fGrindEQ__7_ и перепишем его как $ctg\left(\alpha -\phi \right)=\dfrac{\dot{r}}{r\dot{\phi }} $. Дифференцируя обе части по времени, получаем отсюда $-\dfrac{\dot{\alpha }-\dot{\phi }}{\sin ^{2} \left(\alpha -\phi \right)} =\dfrac{d}{dt} \left(\dfrac{\dot{r}}{r\dot{\phi }} \right)$. Раскрывая здесь правую часть, имеем
$$ \label{GrindEQ__11_}-\frac{\dot{\alpha }-\dot{\phi }}{\sin ^{2} \left(\alpha -\phi \right)} =\frac{d}{dt} \left(\frac{\dot{r}}{r\dot{\phi }} \right)=\frac{\ddot{r}r\dot{\phi }-\dot{r}^{2} \dot{\phi }-r\dot{r}\ddot{\phi }}{r^{2} \dot{\phi }^{2} } .
$$
Сравнивая найденное выражение с уравнением fGrindEQ__10_, и, учитывая условие $\dot{\alpha }-\dot{\phi }\ne 0$, легко получить следующее равенство $\sin ^{2} \left(\alpha -\phi \right)=\dfrac{r^{2} \dot{\phi }^{2} }{v^{2} } $. Или
$$ \label{GrindEQ__12_}r\dot{\phi }=v\sin\left(\alpha -\phi \right).
$$
А так как $\operatorname{ctg}\left(\alpha -\phi \right)=\dfrac{\dot{r}}{r\dot{\phi }} $, то
$$ \label{GrindEQ__13_}\dot{r}=v\cos\left(\alpha -\phi \right).
$$
Для того, чтобы система уравнений была замкнутой, нам осталось найти уравнение для угла $\alpha $. Однако перед тем, как это сделать, необходимо остановиться на одном важном моменте. Поскольку сила реакции есть $N=\frac{mv^{2} }{R} -mg\cos \alpha $, то, полагая (доказательство см. в [9]), что $\dfrac{mv^{2} }{R} =-mg\cos \alpha $ из верхнего уравнения fGrindEQ__2_ найдем
$$ \label{GrindEQ__14_}\dot{v}+\frac{k_{2} }{m} v=g\left(\sin \alpha -2k_{1} \cos \alpha \right). $$
Соответственно сила реакции должна меняться по закону
$$ \label{GrindEQ__15_}N=2mg\cos \alpha .$$
Для простейшего случая замкнутого движения по вертикально стоящему желобу в виде окружности, то есть при $r=R_{0} =\text{const}$ и $\alpha =\phi +\dfrac{\pi }{2} $, видим, что уравнение fGrindEQ__13_ удовлетворяется автоматически, а fGrindEQ__12_ дает известную формулу $v=R_{0} \dot{\phi }$. Это, в свою очередь, приводит к тому, что уравнение fGrindEQ__14_ может быть записано в виде следующего нелинейного дифференциального уравнения
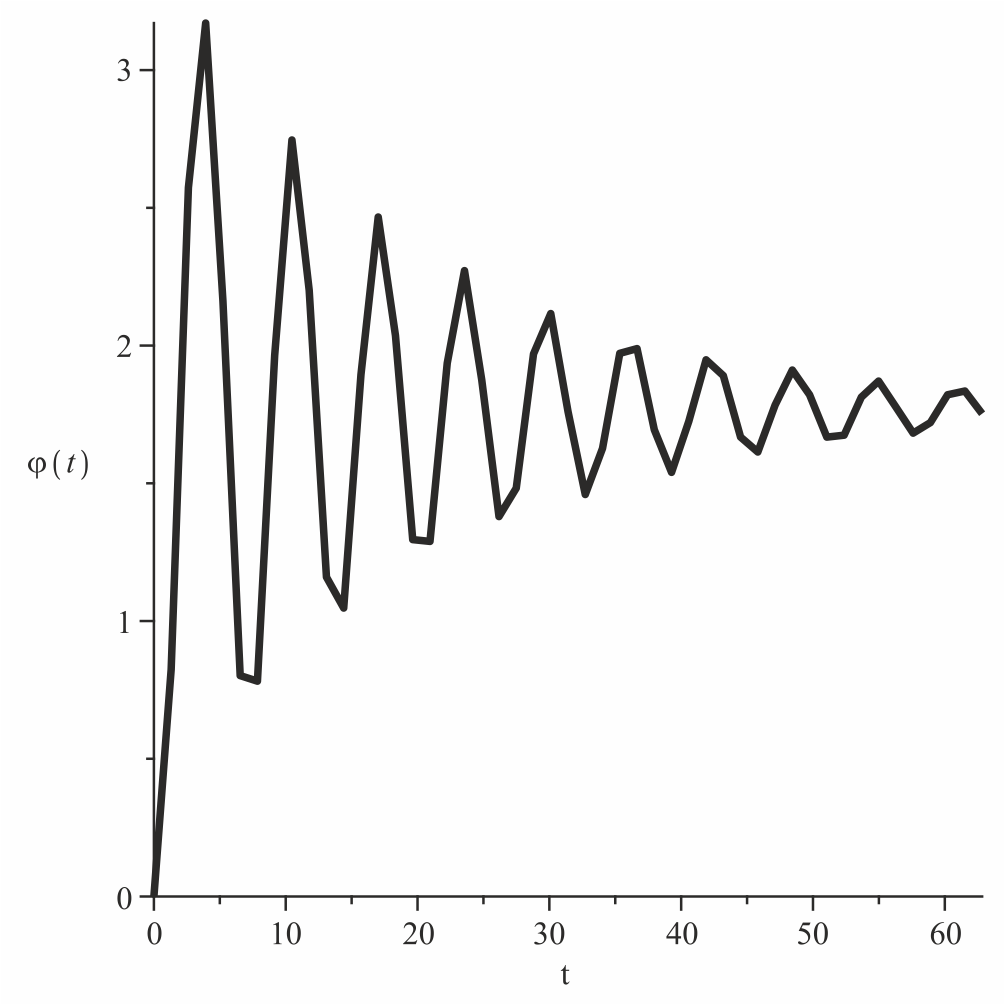
$$ \label{GrindEQ__16_}\ddot{\phi }+\frac{k_{2} }{m} \dot{\phi }-\omega _{0}^{2} \left(\cos \phi +2k_{1} \sin \phi \right)=0,
$$
где частота $\omega _{0} =\sqrt{\dfrac{g}{R_{0} } } $. Уравнение fGrindEQ__16_ было решено численно. В результате получаются затухающие решения, одно из которых мы представили на рис. 2. Обычно коэффициент вязкого трения для реальных размеров тел (но только не в случае нанообъектов (см. ниже)) всегда мал. Несколько подобный подход был продемонстрирован и в задаче о брахистохроне [8], который привел нас не только к правильным зависимостям, но еще и позволил предсказать геометрический фазовый переход, характерный именно для брахистохроны. При этом временное (или угловое) распределение силы реакции желоба может быть определено по уравнению fGrindEQ__15_, как $N=2mg\cos \alpha \left(t\right)$. Таким образом, принимая за основу доказанное равенство $\dfrac{mv^{2} }{R} =mg\cos \alpha $ (см. [8]) и, вспоминая, что $\dot{\alpha }=\dfrac{v}{R} $, находим в итоге следующую замкнутую система нелинейных дифференциальных уравнений, описывающую движение тела по вертикально расположенному желобу произвольной формы
$$\label{GrindEQ__17_}
\begin{gathered}
\dot{v}+\frac{k_{2} }{m} v=g\left(\sin \alpha -2k_{1} \cos \alpha \right),\\ \dot{\alpha }=\pm \frac{g}{v} \cos \alpha ,\\ \dot{\phi }=\frac{v}{r} \sin \left(\alpha -\phi \right),\\ \dot{r}=v\cos\left(\alpha -\phi \right). \end{gathered} $$
Рис. 2. Численное решение уравнения fGrindEQ__16_ для $k_{2} =0.1$ и $k_{1} =0.1$
РЕШЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ
Найдем решения системы уравнений fGrindEQ__17_ в условиях, когда сопротивление отсутствует. Полагая, что $k_{1} =k_{2} =0$, находим
$$\label{GrindEQ__18_}
\begin{gathered}
\dot{v}=g\sin \alpha ,\quad \dot{\alpha }=\pm \frac{g}{v} \cos \alpha ,\\ \dot{\phi }=\frac{v}{r} \sin \left(\alpha -\phi \right), \quad \dot{r}=v\cos\left(\alpha -\phi \right).\end{gathered}
$$
Как мы знаем (см. [8]), если выбирается знак <<$+$>>, то траектория будет представлять собой параболу, для которой тождественно выполняется условие $N=0$, а если <<$-$>>, то это будет брахистохрона. Предположим, что мы говорим о свободном движении и выбираем знак <<$+$>>. Тогда первые два уравнения решаются элементарно, и мы легко получаем, что
$$ \label{GrindEQ__19_}\alpha =\mathrm{arctg}\left(gt+C_{1} \right),\quad v=\sqrt{\left(gt+C_{1} \right)^{2} +C_{2}^{2} },$$
где $C_{1,2}$ --- константы интегрирования. Полагая здесь $C_{1} =0$, а $C_{2} =v_{0} $ и подставляя результат в третье и четвертое уравнения, находим
$$ \label{GrindEQ__20_} \dot{\phi }=\frac{\left(gt\cos \phi -v_{0} \sin \phi \right)}{r} ,\quad \dot{r}=v_{0} \cos \phi +gt\sin \phi .
$$
В безразмерных переменных $\tau =\dfrac{gt}{v_{0}},\,\, u=\dfrac{gr}{v_{0}^{2}}$ отсюда следует
$$ \label{GrindEQ__21_} \phi '=\frac{\left(\tau \cos \phi -\sin \phi \right)}{u} ,\quad u'=\cos \phi +\tau \sin \phi . $$
Численное интегрирование уравнений fGrindEQ__21_ приводит, как и должно быть, к траектории в виде параболы (см. [8]). В том случае, если в уравнениях fGrindEQ__18_ выбрать знак $-$, то легко получаем, что
$$ \label{GrindEQ__22_}\alpha =\frac{-gt+C_{2} }{C_{1} } ,\quad v=C_{1} \cos \left(\frac{gt-C_{2} }{C_{1} } \right). $$
Полагая здесь $C_{2} =0,\,\, C_{1} =v_{0} $, где $v_{0}$ --- начальная скорость движения, находим
$$\label{GrindEQ__23_}
\begin{gathered} \dot{\phi }=-\frac{v_{0} }{r} \cos \left(\frac{gt}{v_{0} } \right)\sin \left(\frac{gt}{v_{0} } +\phi \right),\\ \dot{r}=v_{0} \cos \left(\frac{gt}{v_{0} } \right)\cos \left(\frac{gt}{v_{0} } +\phi \right).
\end{gathered}$$
В безразмерном виде имеем отсюда
$$ \label{GrindEQ__24_} \phi '=-\frac{1}{u} \cos \tau \sin \left(\tau +\phi \right),\quad u'=\cos \tau \cos \left(\tau +\phi \right).
$$
Численное интегрирование системы уравнений fGrindEQ__24_ дает нам в результате уравнение брахистохроны (см. [8]). Надо сказать, что обобщение уравнений fGrindEQ__17_ на значительно более широкий класс траекторий (форм желоба) может быть получено с помощью простого приема, который заключается в том, чтобы во втором уравнении системы fGrindEQ__17_, где стоят знаки «$+$»--«$-$» ввести обобщающий коэффициент $p$, позволяющий нам получить целый класс новых траекторий. Действительно, в этом случае вместо fGrindEQ__17_ можно написать такую систему
$$\label{GrindEQ__25_}
\begin{gathered} \dot{v}+\frac{k_{2} }{m} v=g\left(\sin \alpha -2k_{1} \cos \alpha \right),\quad \dot{\alpha }=p\frac{g}{v} \cos \alpha ,\\ \dot{\phi }=\frac{v}{r} \sin \left(\alpha -\phi \right),\quad \dot{r}=v\cos\left(\alpha -\phi \right).
%\begin{gathered} \dot{\phi }=-\frac{v_{0} }{r} \cos \left(\frac{gt}{v_{0} } \right)\sin \left(\frac{gt}{v_{0} } +\phi \right),\\ %\dot{r}=v_{0} \cos \left(\frac{gt}{v_{0} } \right)\cos \left(\frac{gt}{v_{0} } +\phi \right).
\end{gathered}$$
А в отсутствии трения, соответственно
$$\label{GrindEQ__26_}
\begin{gathered} \dot{v}=g\sin \alpha ,\quad \dot{\alpha }=p\frac{g}{v} \cos \alpha ,\\ \dot{\phi }=\frac{v}{r} \sin \left(\alpha -\phi \right),\quad \dot{r}=v\cos\left(\alpha -\phi \right).
\end{gathered}$$
Первые два уравнения дают нам решение в виде квадратур. В самом деле, из них следует, что
$$ \label{GrindEQ__27_}v\left(\alpha \right)=\frac{C_{1} }{\left|\cos \alpha \right|^{\frac{1}{p} } }, $$
где $C_{1}$ --- константа интегрирования. Подстановка fGrindEQ__27_ в первое уравнение системы fGrindEQ__26_ приводит нас к неявному решению в виде
$$ \label{GrindEQ__28_}\frac{pgt}{C_{1} } =\int _{\pi/2 }^{\alpha }\frac{d\alpha }{\left|\cos \alpha \right|^{1+\frac{1}{p} } } .
$$
Выбирая константу $C_{1} $ из условий $\alpha \left(0\right)=\pi/2 $, а $v\left(0\right)=v_{0} $, перепишем решение fGrindEQ__28_ в более удобной форме
$$ \label{GrindEQ__29_}\frac{pgt}{v_{0} } =\left(-1\right)^{1/p} \int _{0}^{\frac{\pi}{2} -\alpha }\frac{d\tau }{\cos ^{1+\frac{1}{p} } \tau }.
$$
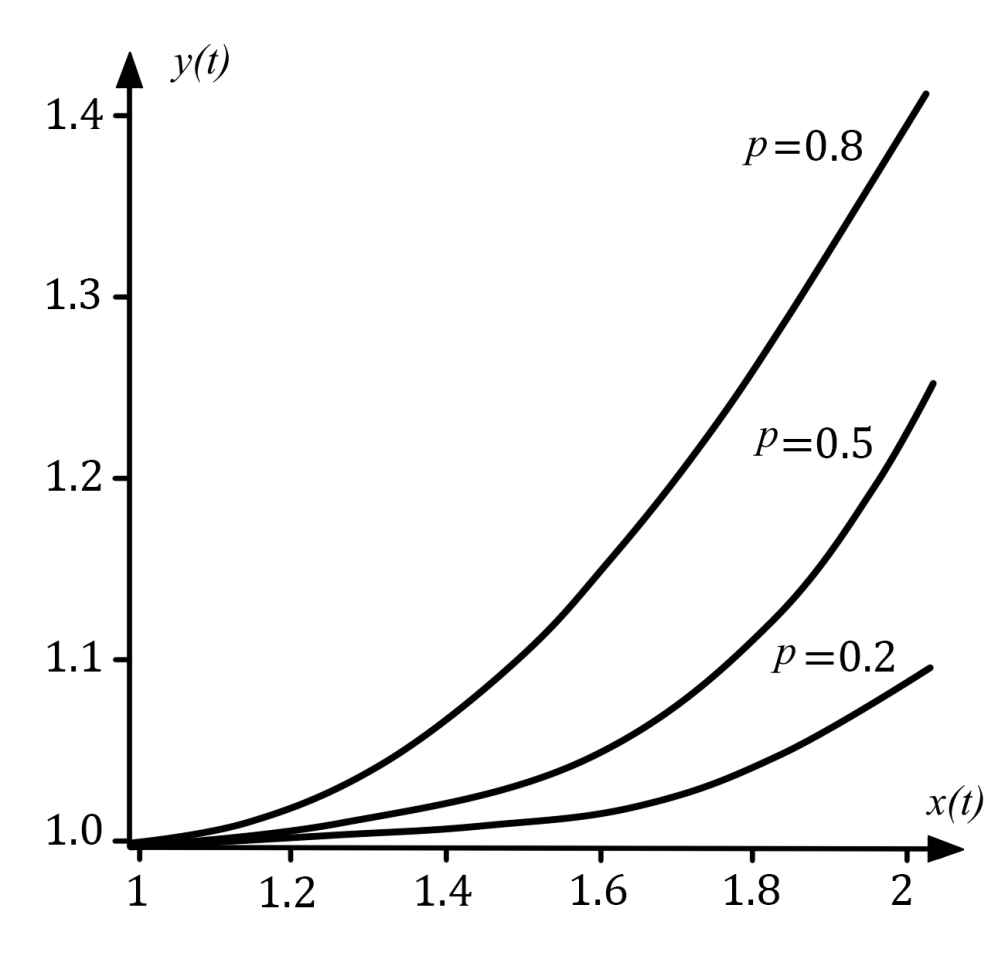
Проанализируем систему уравнений fGrindEQ__26_ в некоторых частных случаях. В случаях $p=\pm 1$ мы знаем, что решения будут приводить нас уравнениям либо параболы ($N=0$), либо к брахистохроне ($N=2mg\cos \alpha $). Положим теперь, что $p=-\dfrac{1}{2} $. В этом случае элементарное интегрирование в fGrindEQ__29_ дает нам решение $\sin \alpha =-\dfrac{gt}{2v_{0} } $ или $\alpha =2\pi n-\arcsin \left(\dfrac{gt}{2v_{0} } \right)$. Видно, что решение периодическое, но при этом у нас имеется еще и ограничение на угол $\alpha $, а именно $0\le \alpha \le \dfrac{\pi }{2} $. Это означает, что $0 \le 2n-\dfrac{1}{\pi } \arcsin \left(\dfrac{gt}{2v_{0} } \right)\le \dfrac{1}{2} $. Как отсюда видно, полученное неравенство не может быть выполнено ни при каких значениях $t$. Таким образом, при $p<0$ решений не существует. При положительных значениях параметра $p$ анализ трех частных случаев показан на рис. 3.
Если в общих уравнениях fGrindEQ__17_ ввести безразмерные функции $y_{1} =\dfrac{v}{v_{0} } $, $y_{2} =\phi $, $y_{3} =\alpha $, $y_{4} =\dfrac{r}{r_{0} } $, где $r_{0} =\dfrac{v_{0}^{2} }{g} $, а $t=\dfrac{v_{0} }{g} \tau $, то вместо системы fGrindEQ__17_ получим такую
$$\label{GrindEQ__30_}
\begin{gathered}
y'_{1} +\mu y_{1} =\sin y_{3} -2k_{1} \cos y_{3} ,\quad y'_{3} =\frac{\cos y_{3} }{y_{1} } ,\\ y'_{2} =\frac{y_{1} }{y_{4} } \sin \left(y_{3} -y_{2} \right),\quad y'_{4} =y_{1} \cos \left(y_{3} -y_{2} \right).
\end{gathered}
$$
где новый безразмерный параметр $\mu =\dfrac{k_{2} v_{0} }{mg} $, а $k_{1}$ --- обычный безразмерный коэффициент сухого трения, характерные значения которого принадлежат области $k_{1} =\left(0,1\div 1\right)$. Что касается коэффициента $\mu $, то его значения должны определяться линейными размерами тела. Действительно, поскольку масса $m=\rho V$, где $\rho -$ плотность, объем $V\sim L^{3} $, где $L$ --- характерный линейный размер, а коэффициент $k_{2} =\xi \eta L$ (см. выше), то $\mu =\xi \dfrac{\eta v_{0} }{\rho L^{2} g} $, и в случае малых частиц (от $10^{-2} \div 10^{-5} $ см.) имеем $\mu \sim 1\div 10^{3} $. Для частиц большего размера (от $1\div 10^{-1}$ см.) находим, что $\mu \sim 10^{-4} \div 10^{-2} $. То есть для случая наночастиц сопротивление Стокса становится очень большим. Это означает, что в случае нанообъектов формулой Стокса пользоваться нельзя, и для них существует некоторое ограничение на линейный критический размер $R_{cr} $, выше которого должна «работать» формула Стокса, а ниже этого значения следует использовать метод кинетического уравнения Больцмана. Критерием здесь может служить равенство $l=R_{cr} $, где $l$ --- длина свободного пробега молекулы.
ЗАКЛЮЧЕНИЕ
В заключении работы обратим еще раз внимание на ряд результатов полученных выше.
- Получена общая система уравнений движений для плоского криволинейного движения.
- Дано обобщение системы уравнений в отсутствии трения на произвольные соотношения между $\dfrac{v^{2} }{R} $ и $g\cos \alpha $ с помощью введенного параметра $p$. При этом доказано, что для значений $-1<p<0$ решений не существует, а для некоторых значений $p>0$ численные решения показаны на рис. 3.
- Приведено решение системы fGrindEQ__18_ в отсутствии сопротивления в двух случаях: $p=1$ --- свободное движение ($N=0$) и $p=-1$ --- движение по брахистохроне ($N=2mg\cos \alpha $).
- Ландау Л. Д., Лифшиц Е. М. Курс теоретической физики. Механика. М.: Наука, 1988.
- Сивухин Д. В. Общий курс физики. Механика. М.: Физматлит, 2010.
- Лурье А. И. Аналитическая механика. М.: Физмалит, 1961.
- Гантмахер Ф. Р. Лекции по аналитической механике. М.: Наука, 1966.
- Добронравов В. В. Основы аналитической механики. М.: Высшая школа, 1976.
- Коткин Г. Л., Черных А. И., Сербо В. Г. Лекции по аналитической механике. Ижевск. РХД. 2010.
- Гладков С. О. Ученые записки Московского ун-та. 2016. № 4. 164101.
- Гладков С. О., Богданова С. Б.
Ученые записки Московского ун-та. 2016. № 1. 161001.
Generalized dynamical equations of plane curvilinear motion of a material body on a trench with account of a friction forces (their numerical analysis in some special cases)
S. O. Gladkov$^{a}$, S. B. Bogdanova$^{b}$
Moscow Aviation Institute (National Research University) (MAI).
Moscow 125993 Russia
E-mail: $^a$sglad@newmail.ru, $^b$sonjaf@list.ru.
In this paper we have derived the general dynamic equations of a plane curvilinear motion, taking into account the forces as a viscous as and dry friction. It's founded a closed system of four nonlinear differential equations. Its analyzes of the solution in some special cases illustrated by the graphical in the view of different trajectories which charactering of the plane motion.
PACS: 05.45.-a.
Keywords: curvilinear motion, the law of conservation of angular momentum, nonlinear dynamic equations.
Received 11 October 2016.
Сведения об авторах
- Гладков Сергей Октябринович --- доктор физ.-мат. наук, профессор; тел.: (499) 158-46-47, e-mail: sglad@newmail.ru.
- Богданова Софья Борисовна --- кандидат физ.-мат. наук, доцент; тел.: (499) 158-46-47, e-mail: sonjaf@list.ru.